My Ph.D. dissertation was focused on developing a mathematical model to simulate droplet formation process under various external force, like gravity, shear, etc. We see droplets forming in many natural and industrial settings. Rain drops and wave breakup into tiny droplets being examples of natural occurrence while ink-jet printing, emulsion, atomization in hybrid rocket engine, etc. are examples in industrial processes.
First, I developed a computational model to simulate a straight forward example of a droplet formation under a gravitational force. This model was implemented in C programming language using an open-source library PETSc. A self-consistent algorithm to calculate the length of a moving droplet was included in the model. The validation was performed using the previous experimental study on water and 85% glycerol solution.
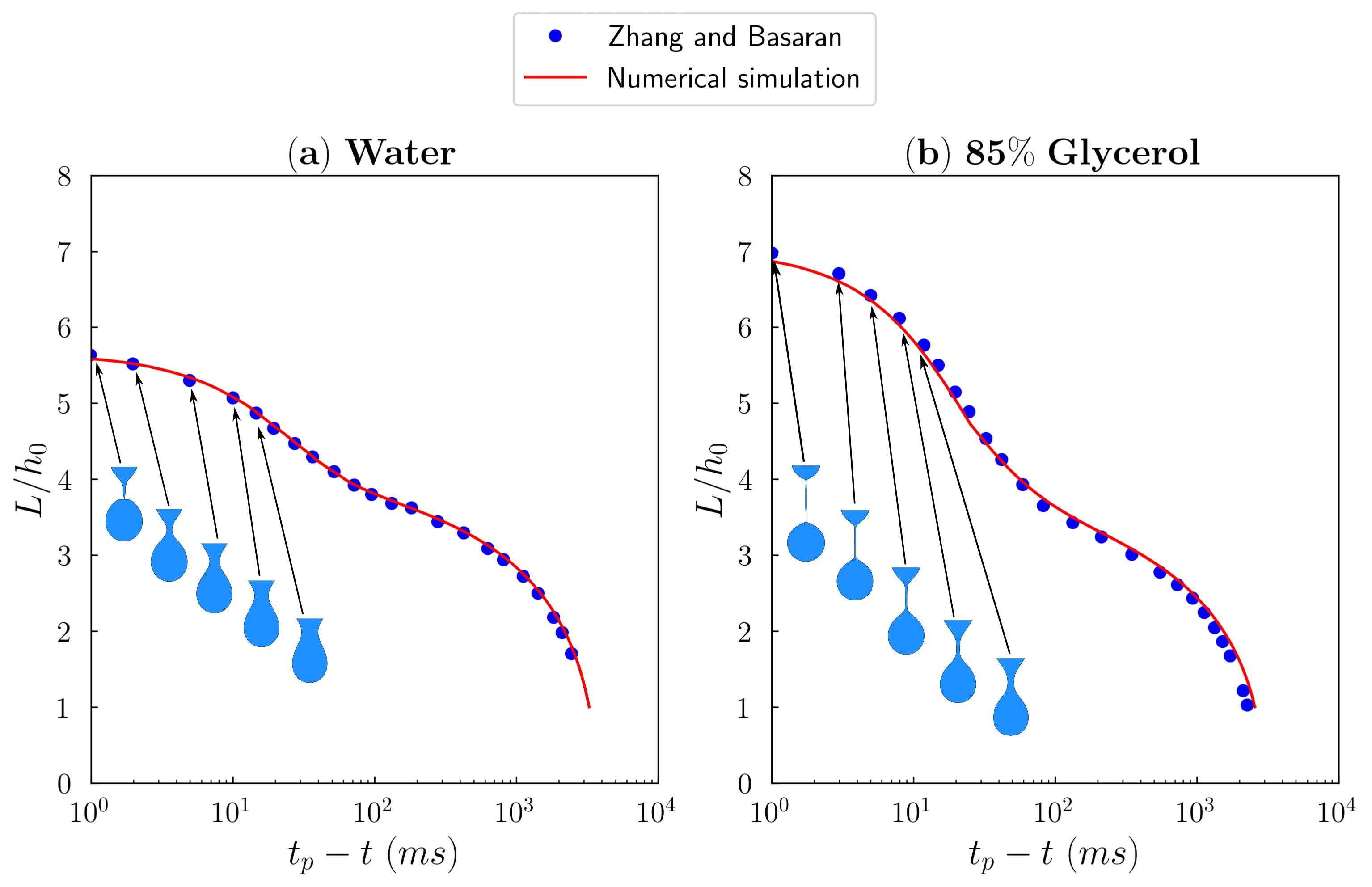
The evolution of these droplets can be seen in the following animations. An interesting part of this model is that a simplification of the Navier-Stokes equations using asymptotic expansion leads to an elegant one-dimensional momentum equation and this, along with the interface tracking, is capable of capturing the droplet evolution and pinch-off time very accurately.